By definition, a fluid is any substance that is able to flow if it is not in some way confined or restricted. Liquids and gases are both classified as fluids, and often act in a very similar way. One significant difference comes into play when a force is applied to these fluids. In this case, liquids tend to be incompressible and gases are highly compressible. Many of the principles that aviation is based on, such as the theory of lift on a wing and the force generated by a hydraulic system, can be explained and quantified by using the laws of fluid mechanics.
The following experiment is illustrated in Figure 1. The overflow can is filled to the spout with water. The heavy metal cube is first weighed in still air and weighs 10 lb. It is then weighed while completely submerged in the water and it weighs 3 lb. The difference between the two weights is the buoyant force of the water. As the cube is lowered into the overflow can, the water is caught in the catch bucket. The volume of water which overflows equals the volume of the cube. The volume of irregular shaped objects can also be measured by using this method. If this experiment is performed carefully, the weight of the water displaced by the metal cube exactly equals the buoyant force of the water, which the scale shows to be 7 lb.
Still thinking about Figure 4, if the pressure was measured half way down, it would be half of 8.34, or 4.17 psi. In other words, the pressure is adjustable by varying the height of the column. Pressure based on the column height of a fluid is known as static pressure. With liquids, such as gasoline, it is sometimes referred to as a head of pressure. For example, if a carburetor needs to have 2 psi supplied to its inlet, or head of pressure, this could be accomplished by having the fuel tank positioned the appropriate number of inches higher than the carburetor.
As identified in the previous paragraph, pressure due to the height of a fluid column is known as static pressure. When a fluid is in motion, and its velocity is converted to pressure, that pressure is known as ram. When ram pressure and static pressure are added together, the result is known as total pressure. In the inlet of a gas turbine engine, for example, total pressure is often measured to provide a signal to the fuel metering device or to provide a signal to a gauge on the flight deck.
In Figure 4, if a piston is placed at the top of the cylinder and an external force pushes down on the piston, additional pressure will be created in the liquid. If the additional pressure is 100 psi, this 100 psi will act equally and undiminished from the top of the cylinder all the way to the bottom. The gauge at the bottom will now read 108.34 psi, and if a gauge were positioned half way down the cylinder, it would read 104.17 psi, which is found by adding 100 plus half of 8.34.
Pascal’s law, when dealing with the variables of force, pressure, and area, is dealt with by way of the following formula.
Force = Pressure × Area
In this formula, the force is in units of pounds, the pressure is in pounds per square inch (psi), and the area is in square inches. By transposing the original formula, we have two additional formulas, as follows:
Pressure = Force ÷ Area
and
Area = Force ÷ Pressure
An easy and convenient way to remember the formulas for Pascal’s law, and the relationship between the variables, is with the triangle shown in Figure 5. If the variable we want to solve for is covered up, the position of the remaining two variables shows the proper math relationship. For example, if the “A,” or area, is covered up, what remains is the “F” on the top and the “P” on the bottom, meaning force divided by pressure.
The simple hydraulic system in Figure 6 has 5 lb force acting on a piston with a 1⁄2 in2 surface area. Based on Pascal’s law, the pressure in the system would be equal to the force applied divided by the area of the piston, or 10 psi. As shown in Figure 6, the pressure of 10 psi is present everywhere in the fluid.
The hydraulic system in Figure 7 is a little more complex than the one in Figure 6. In Figure 7, the input force of 5 lb is acting on a 1⁄2-in2 piston, creating a pressure of 10 psi. The input cylinder and piston is connected to a second cylinder, which contains a 5-in2 piston. The pressure of 10 psi created by the input piston pushes on the piston in the second cylinder, creating an output force of 50 pounds.
Often, the purpose of a hydraulic system is to generate a large output force, with the input force being much less. In Figure 7, the input force is 5 lb and the output force is 50 lb, or 10 times greater. The relationship between the output force and the input force is known as mechanical advantage. The mechanical advantage in Figure 7 would be 50 divided by 5, or 10. The following formulas can be used to calculate mechanical advantage.
Mechanical Advantage = Force Out ÷ Force In
or
Mechanical Advantage = Distance Out ÷ Distance In
Earlier in this section when simple machines, such as levers and gears were discussed, it was identified that no machine allows us to gain work. The same statement holds true for a hydraulic system, that we get no more work out of a hydraulic system than we put in. Since work is equal to force times distance, if we gain force with a hydraulic system, we must lose distance. We only get the same work out, if the system is 100 percent efficient.
Buoyancy
A solid body submerged in a liquid or a gas weighs less than when weighed in free space. This is because of the upward force, called buoyant force, which any fluid exerts on a body submerged in it. An object will float if this upward force of the fluid is greater than the weight of the object. Objects denser than the fluid, even though they sink readily, appear to lose a part of their weight when submerged. A person can lift a larger weight under water than he or she can possibly lift in the air.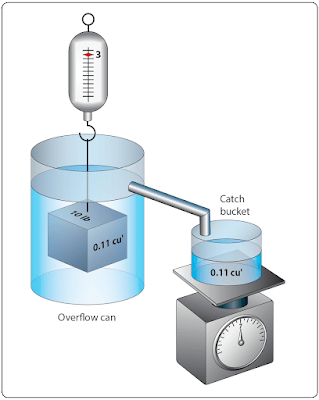 |
| Figure 1. Example of buoyancy |
The following experiment is illustrated in Figure 1. The overflow can is filled to the spout with water. The heavy metal cube is first weighed in still air and weighs 10 lb. It is then weighed while completely submerged in the water and it weighs 3 lb. The difference between the two weights is the buoyant force of the water. As the cube is lowered into the overflow can, the water is caught in the catch bucket. The volume of water which overflows equals the volume of the cube. The volume of irregular shaped objects can also be measured by using this method. If this experiment is performed carefully, the weight of the water displaced by the metal cube exactly equals the buoyant force of the water, which the scale shows to be 7 lb.
Archimedes (287–212 B.C.) performed similar experiments. As a result, he discovered that the buoyant force which a fluid exerts upon a submerged body is equal to the weight of the fluid the body displaces. This statement is referred to as Archimedes’ principle. This principle applies to all fluids, gases as well as liquids. Just as water exerts a buoyant force on submerged objects, air exerts a buoyant force on objects submerged in it.
The amount of buoyant force available to an object can be calculated by using the following formula:
Buoyant Force = Volume of Object × Density of Fluid Displaced
If the buoyant force is more than the object weighs, the object will float. If the buoyant force is less than the object weighs, the object will sink. For the object that sinks, its measurable weight will be less by the weight of the displaced fluid.
Example: A 10-ft3 object weighing 700 lb is placed in pure water. Will the object float? If the object sinks, what is its measurable weight in the submerged condition? If the object floats, how many cubic feet of its volume is below the water line?
Buoyant Force = Volume of Object × Density of Fluid Displaced
= 10 (62.4)
= 624 lb
The object will sink because the buoyant force is less than the object weighs. The difference between the buoyant force and the object’s weight will be its measurable weight, or 76 lb.
Two good examples of buoyancy are a helium filled airship and a seaplane on floats. An airship is able to float in the atmosphere and a seaplane is able to float on water. That means both have more buoyant force than weight. Figure 2 is a DeHavilland Twin Otter seaplane, with a gross takeoff weight of 12,500 lb. At a minimum, the floats on this airplane must be large enough to displace a weight in water equal to the airplane’s weight. According to Title 14 of the Code of Federal Regulations (14 CFR) part 23, the floats must be 80 percent larger than the minimum needed to support the airplane.
For this airplane, the necessary size of the floats would be calculated as follows:
Divide the airplane weight by the density of water.
12,500 ÷ 62.4 = 200.3 ft3
Multiply this volume by 80%.
200.3 × 80% = 160.2 ft3
Add the two volumes together to get the total volume of the floats.
200.3 + 160.2 = 360.5 ft3
By looking at the Twin Otter in Figure 2, it is obvious that much of the volume of the floats is out of the water. This is accomplished by making sure the floats have at least 80 percent more volume than the minimum necessary.
The amount of buoyant force available to an object can be calculated by using the following formula:
Buoyant Force = Volume of Object × Density of Fluid Displaced
If the buoyant force is more than the object weighs, the object will float. If the buoyant force is less than the object weighs, the object will sink. For the object that sinks, its measurable weight will be less by the weight of the displaced fluid.
Example: A 10-ft3 object weighing 700 lb is placed in pure water. Will the object float? If the object sinks, what is its measurable weight in the submerged condition? If the object floats, how many cubic feet of its volume is below the water line?
Buoyant Force = Volume of Object × Density of Fluid Displaced
= 10 (62.4)
= 624 lb
The object will sink because the buoyant force is less than the object weighs. The difference between the buoyant force and the object’s weight will be its measurable weight, or 76 lb.
Two good examples of buoyancy are a helium filled airship and a seaplane on floats. An airship is able to float in the atmosphere and a seaplane is able to float on water. That means both have more buoyant force than weight. Figure 2 is a DeHavilland Twin Otter seaplane, with a gross takeoff weight of 12,500 lb. At a minimum, the floats on this airplane must be large enough to displace a weight in water equal to the airplane’s weight. According to Title 14 of the Code of Federal Regulations (14 CFR) part 23, the floats must be 80 percent larger than the minimum needed to support the airplane.
 |
| Figure 2. DeHavilland Twin Otter seaplane |
For this airplane, the necessary size of the floats would be calculated as follows:
Divide the airplane weight by the density of water.
12,500 ÷ 62.4 = 200.3 ft3
Multiply this volume by 80%.
200.3 × 80% = 160.2 ft3
Add the two volumes together to get the total volume of the floats.
200.3 + 160.2 = 360.5 ft3
By looking at the Twin Otter in Figure 2, it is obvious that much of the volume of the floats is out of the water. This is accomplished by making sure the floats have at least 80 percent more volume than the minimum necessary.
Some of the large Goodyear airships have a volume of 230,000 ft3. Since the fluid they are submerged in is air, to find the buoyant force of the airship, the volume of the airship is multiplied by the density of air (.07651 lb⁄ft3). For this Goodyear airship, the buoyant force is 17,597 lb. Figure 3 shows an inside view of the Goodyear airship.
The forward and aft ballonets are air chambers within the airship. Through the air scoop, air can be pumped into the ballonets or evacuated from the ballonets in order to control the weight of the airship. Controlling the weight of the airship controls how much positive or negative lift it has. Although the airship is classified as a lighter-than-air aircraft, it is in fact flown in a condition slightly heavier than air.
 |
| Figure 3. The Goodyear Airship and buoyancy |
The forward and aft ballonets are air chambers within the airship. Through the air scoop, air can be pumped into the ballonets or evacuated from the ballonets in order to control the weight of the airship. Controlling the weight of the airship controls how much positive or negative lift it has. Although the airship is classified as a lighter-than-air aircraft, it is in fact flown in a condition slightly heavier than air.
Fluid Pressure
The pressure exerted on the bottom of a container by a liquid is determined by the height of the liquid and not by the shape of the container. This can be seen in Figure 4, where three different shapes and sizes of containers are full of colored water. Even though they are different shapes and have different volumes of liquid, each one has a height of 231 inches. Each one would exert a pressure on the bottom of 8.34 psi because of this height. The container on the left, with a surface area of 1 in2, contains a volume of 231 in3 (one gallon). One gallon of water weighs 8.34 lb, which is why the pressure on the bottom is 8.34 psi. |
| Figure 4. Fluid pressure based on column height |
Still thinking about Figure 4, if the pressure was measured half way down, it would be half of 8.34, or 4.17 psi. In other words, the pressure is adjustable by varying the height of the column. Pressure based on the column height of a fluid is known as static pressure. With liquids, such as gasoline, it is sometimes referred to as a head of pressure. For example, if a carburetor needs to have 2 psi supplied to its inlet, or head of pressure, this could be accomplished by having the fuel tank positioned the appropriate number of inches higher than the carburetor.
As identified in the previous paragraph, pressure due to the height of a fluid column is known as static pressure. When a fluid is in motion, and its velocity is converted to pressure, that pressure is known as ram. When ram pressure and static pressure are added together, the result is known as total pressure. In the inlet of a gas turbine engine, for example, total pressure is often measured to provide a signal to the fuel metering device or to provide a signal to a gauge on the flight deck.
Pascal’s Law
The foundations of modern hydraulics and pneumatics were established in 1653 when Pascal discovered that pressure set up in a fluid acts equally in all directions. This pressure acts at right angles to containing surfaces. When the pressure in the fluid is caused solely by the fluid’s height, the pressure against the walls of the container is equal at any given level, but it is not equal if the pressure at the bottom is compared to the pressure half way down. The concept of the pressure set up in a fluid, and how it relates to the force acting on the fluid and the surface area through which it acts, is Pascal’s law.In Figure 4, if a piston is placed at the top of the cylinder and an external force pushes down on the piston, additional pressure will be created in the liquid. If the additional pressure is 100 psi, this 100 psi will act equally and undiminished from the top of the cylinder all the way to the bottom. The gauge at the bottom will now read 108.34 psi, and if a gauge were positioned half way down the cylinder, it would read 104.17 psi, which is found by adding 100 plus half of 8.34.
Pascal’s law, when dealing with the variables of force, pressure, and area, is dealt with by way of the following formula.
Force = Pressure × Area
In this formula, the force is in units of pounds, the pressure is in pounds per square inch (psi), and the area is in square inches. By transposing the original formula, we have two additional formulas, as follows:
Pressure = Force ÷ Area
and
Area = Force ÷ Pressure
An easy and convenient way to remember the formulas for Pascal’s law, and the relationship between the variables, is with the triangle shown in Figure 5. If the variable we want to solve for is covered up, the position of the remaining two variables shows the proper math relationship. For example, if the “A,” or area, is covered up, what remains is the “F” on the top and the “P” on the bottom, meaning force divided by pressure.
 |
| Figure 5. Force, area, pressure relationship |
The simple hydraulic system in Figure 6 has 5 lb force acting on a piston with a 1⁄2 in2 surface area. Based on Pascal’s law, the pressure in the system would be equal to the force applied divided by the area of the piston, or 10 psi. As shown in Figure 6, the pressure of 10 psi is present everywhere in the fluid.
 |
| Figure 6. Pressure created in a hydraulic system |
The hydraulic system in Figure 7 is a little more complex than the one in Figure 6. In Figure 7, the input force of 5 lb is acting on a 1⁄2-in2 piston, creating a pressure of 10 psi. The input cylinder and piston is connected to a second cylinder, which contains a 5-in2 piston. The pressure of 10 psi created by the input piston pushes on the piston in the second cylinder, creating an output force of 50 pounds.
 |
| Figure 7. Output force created in a hydraulic system |
Often, the purpose of a hydraulic system is to generate a large output force, with the input force being much less. In Figure 7, the input force is 5 lb and the output force is 50 lb, or 10 times greater. The relationship between the output force and the input force is known as mechanical advantage. The mechanical advantage in Figure 7 would be 50 divided by 5, or 10. The following formulas can be used to calculate mechanical advantage.
Mechanical Advantage = Force Out ÷ Force In
or
Mechanical Advantage = Distance Out ÷ Distance In
Earlier in this section when simple machines, such as levers and gears were discussed, it was identified that no machine allows us to gain work. The same statement holds true for a hydraulic system, that we get no more work out of a hydraulic system than we put in. Since work is equal to force times distance, if we gain force with a hydraulic system, we must lose distance. We only get the same work out, if the system is 100 percent efficient.
In order to think about the distance that the output piston will move in response to the movement of the input piston, the volume of fluid displaced must be considered. In the study of geometry, one learns that the volume of a cylinder is equal to the cylinder’s surface area multiplied by its height. So, when a piston of 2 in2 moves down in a cylinder a distance of 10 in, it displaces a volume of fluid equal to 20 in3 (2 in2 × 10 in). The 20 in3 displaced by the first piston is what moves over to the second cylinder and causes its piston to move. In a simple two-piston hydraulic system, the relationship between the piston area and the distance moved is shown by the following formula.
Input Piston Area (Distance Moved) = Output Piston Area (Distance Moved)
As a liquid, or fluid, flows through the venturi tube, the gauges at points “A,” “B,” and “C” are positioned to register the velocity and the static pressure of the liquid. The venturi in Figure 9 can be used to illustrate Bernoulli’s principle, which states that: The static pressure of a fluid, liquid or gas, decreases at points where the velocity of the fluid increases, provided no energy is added to nor taken away from the fluid. The velocity of the air is kinetic energy and the static pressure of the air is potential energy.
In the wide section of the venturi (points A and C of Figure 9), the liquid moves at low velocity, producing a high static pressure, as indicated by the pressure gauge. As the tube narrows in the center, it must contain the same volume of fluid as the two end areas. As indicated by the velocity gauge reading high and the pressure gauge reading low, in this narrow section, the liquid moves at a higher velocity, producing a lower pressure than that at points A and C. A good application for the use of the venturi principle is in a float-type carburetor. As the air flows through the carburetor on its way to the engine, it goes through a venturi, where the static pressure is reduced. The fuel in the carburetor, which is under a higher pressure, flows into the lower pressure venturi area and mixes with the air.
Bernoulli’s principle is extremely important in understanding how some of the systems used in aviation work, including how the wing of an airplane generates lift or why the inlet duct of a turbine engine on a subsonic airplane is diverging in shape. The wing on a slow-moving airplane has a curved top surface and a relatively flat bottom surface. The curved top surface acts like half of the converging shaped middle of a venturi. As the air flow over the top of the wing, the air speeds up, and its static pressure decreases. The static pressure on the bottom of the wing is now greater than the pressure on the top, and this pressure difference creates the lift on the wing. Bernoulli’s principle and the concept of lift on a wing are covered in greater depth in “Aircraft Theory of Flight” post.
RELATED POSTS
Input Piston Area (Distance Moved) = Output Piston Area (Distance Moved)
This formula shows that the volume in is equal to the volume out. This concept is shown in Figure 8, where a small input piston moves a distance of 20 inches, and the larger output piston only moves a distance of 1 inch.
Example: A two-piston hydraulic system, like that shown in Figure 8, has an input piston with an area of 1⁄4 in2 and an output piston with an area of 15 in2. An input force of 50 lb is applied, and the input piston moves 30 inches. What is the pressure in the system, how much force is generated by the output piston, how far would the output piston move, and what is the mechanical advantage?
Pressure = Force ÷ Area
= 50 ÷ 1⁄4
= 200 psi
Force = Pressure × Area
= 200 × 15
= 3,000 lb
Mechanical Advantage = Force Out ÷ Force In
= 3,000 ÷ 50
= 60
Input Piston Area (Distance Moved) = Output Piston Area (Distance Moved)
1⁄4 (30) = 15 (Distance Moved)
1⁄4 (30) ÷ 15 = Distance Moved Distance Moved = 1⁄2 in
Part of understanding Pascal’s law and hydraulics involves utilizing formulas, and recognizing the relationship between the individual variables. Before the numbers are plugged into the formulas, it is often possible to analyze the variables in the system and come to a realization about what is happening. For example, look at the variables in Figure 8 and notice that the output piston is 20 times larger than the input piston, 5 in2 compared to 1⁄4 in2. That comparison tells us that the output force will be 20 times greater than the input force, and also that the output piston will only move 1⁄20 as far. Without doing any formula based calculations, we can conclude that the hydraulic system in question has a mechanical advantage of 20.
 |
| Figure 8. Piston movement in a hydraulic system |
Example: A two-piston hydraulic system, like that shown in Figure 8, has an input piston with an area of 1⁄4 in2 and an output piston with an area of 15 in2. An input force of 50 lb is applied, and the input piston moves 30 inches. What is the pressure in the system, how much force is generated by the output piston, how far would the output piston move, and what is the mechanical advantage?
Pressure = Force ÷ Area
= 50 ÷ 1⁄4
= 200 psi
Force = Pressure × Area
= 200 × 15
= 3,000 lb
Mechanical Advantage = Force Out ÷ Force In
= 3,000 ÷ 50
= 60
Input Piston Area (Distance Moved) = Output Piston Area (Distance Moved)
1⁄4 (30) = 15 (Distance Moved)
1⁄4 (30) ÷ 15 = Distance Moved Distance Moved = 1⁄2 in
Part of understanding Pascal’s law and hydraulics involves utilizing formulas, and recognizing the relationship between the individual variables. Before the numbers are plugged into the formulas, it is often possible to analyze the variables in the system and come to a realization about what is happening. For example, look at the variables in Figure 8 and notice that the output piston is 20 times larger than the input piston, 5 in2 compared to 1⁄4 in2. That comparison tells us that the output force will be 20 times greater than the input force, and also that the output piston will only move 1⁄20 as far. Without doing any formula based calculations, we can conclude that the hydraulic system in question has a mechanical advantage of 20.
Bernoulli’s Principle
Bernoulli’s principle was originally stated to explain the action of a liquid flowing through the varying cross-sectional areas of tubes. In Figure 9 a tube is shown in which the cross-sectional area gradually decreases to a minimum diameter in its center section. A tube constructed in this manner is called a “venturi,” or “venturi tube.” Where the cross-sectional area is decreasing, the passageway is referred to as a converging duct. As the passageway starts to spread out, it is referred to as a diverging duct.
 |
| Figure 9. Bernoulli’s principle and a venturi |
As a liquid, or fluid, flows through the venturi tube, the gauges at points “A,” “B,” and “C” are positioned to register the velocity and the static pressure of the liquid. The venturi in Figure 9 can be used to illustrate Bernoulli’s principle, which states that: The static pressure of a fluid, liquid or gas, decreases at points where the velocity of the fluid increases, provided no energy is added to nor taken away from the fluid. The velocity of the air is kinetic energy and the static pressure of the air is potential energy.
In the wide section of the venturi (points A and C of Figure 9), the liquid moves at low velocity, producing a high static pressure, as indicated by the pressure gauge. As the tube narrows in the center, it must contain the same volume of fluid as the two end areas. As indicated by the velocity gauge reading high and the pressure gauge reading low, in this narrow section, the liquid moves at a higher velocity, producing a lower pressure than that at points A and C. A good application for the use of the venturi principle is in a float-type carburetor. As the air flows through the carburetor on its way to the engine, it goes through a venturi, where the static pressure is reduced. The fuel in the carburetor, which is under a higher pressure, flows into the lower pressure venturi area and mixes with the air.
Bernoulli’s principle is extremely important in understanding how some of the systems used in aviation work, including how the wing of an airplane generates lift or why the inlet duct of a turbine engine on a subsonic airplane is diverging in shape. The wing on a slow-moving airplane has a curved top surface and a relatively flat bottom surface. The curved top surface acts like half of the converging shaped middle of a venturi. As the air flow over the top of the wing, the air speeds up, and its static pressure decreases. The static pressure on the bottom of the wing is now greater than the pressure on the top, and this pressure difference creates the lift on the wing. Bernoulli’s principle and the concept of lift on a wing are covered in greater depth in “Aircraft Theory of Flight” post.
RELATED POSTS
