A machine is any device with which work may be accomplished. For example, machines can be used for any of the following purposes, or combinations of these 5 purposes:
There are only six simple machines. They are the lever, the pulley, the wheel and axle, the inclined plane, the screw, and the gear. Physicists, however, recognize only two basic principles in machines: the lever and the inclined plane. The pulley (block and tackle), the wheel and axle, and gears operate on the machine principle of the lever. The wedge and the screw use the principle of the inclined plane.
An understanding of the principles of simple machines provides a necessary foundation for the study of compound machines, which are combinations of two or more simple machines.
In reference to machines, mechanical advantage is a comparison of the output force to the input force, or the output distance to the input distance. If there is a mechanical advantage in terms of force, there will be a fractional disadvantage in terms of distance. The following formulas can be used to calculate mechanical advantage.
Mechanical Advantage = Force Out ÷ Force In
or
Mechanical Advantage = Distance Out ÷ Distance In
When calculating how much effort is required to lift a specific weight, or how much weight can be lifted by a specific effort, the following formula can be used.
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l) What this formula really shows is the input torque (effort × effort arm) equals the output torque (resistance × resistance arm). This formula and concept apply to all three classes of levers and to all simple machines in general.
Example: A first class lever is to be used to lift a 500-lb weight. The distance from the weight to the fulcrum is 12 inches and from the fulcrum to the applied effort is 60 inches. How much force is required to lift the weight?
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l)
E × 60 in = 500 lb × 12 in
E = 500 lb × 12 in ÷ 60 in
E = 100 lb
The mechanical advantage of the lever in this example would be:
Mechanical Advantage = Force Out ÷ Force In
= 500 lb ÷ 100 lb
= 5, or 5 to 1
An interesting thing to note with this example lever is if the applied effort moved down 10 inches, the weight on the other end would only move up 2 inches. The weight being lifted would only move one-fifth as far. The reason for this is the concept of work. If it allows you to lift 5 times more weight, you will only move it 1⁄5 as far as you move the effort, because a lever cannot have more work output than input.
- Machines are used to transform energy, as in the case of a generator transforming mechanical energy into electrical energy.
- Machines are used to transfer energy from one place to another, as in the examples of the connecting rods, crankshaft, and reduction gears transferring energy from an aircraft’s engine to its propeller.
- Machines are used to multiply force; for example, a system of pulleys may be used to lift a heavy load. The pulley system enables the load to be raised by exerting a force that is smaller than the weight of the load.
- Machines can be used to multiply speed. A good example is the bicycle, by which speed can be gained by exerting a greater force.
- Machines can be used to change the direction of a force. An example of this use is the flag hoist. A downward force on one side of the rope exerts an upward force on the other side, raising the flag toward the top of the pole.
There are only six simple machines. They are the lever, the pulley, the wheel and axle, the inclined plane, the screw, and the gear. Physicists, however, recognize only two basic principles in machines: the lever and the inclined plane. The pulley (block and tackle), the wheel and axle, and gears operate on the machine principle of the lever. The wedge and the screw use the principle of the inclined plane.
An understanding of the principles of simple machines provides a necessary foundation for the study of compound machines, which are combinations of two or more simple machines.
Mechanical Advantage of Machines
As identified in statements 3 and 4 under simple machines, a machine can be used to multiply force or to multiply speed. It cannot, however, multiply force and speed at the same time. In order to gain one force, it must lose the other force. To do otherwise would mean the machine has more power going out than coming in, and that is not possible.In reference to machines, mechanical advantage is a comparison of the output force to the input force, or the output distance to the input distance. If there is a mechanical advantage in terms of force, there will be a fractional disadvantage in terms of distance. The following formulas can be used to calculate mechanical advantage.
Mechanical Advantage = Force Out ÷ Force In
or
Mechanical Advantage = Distance Out ÷ Distance In
The Lever
The simplest machine, and perhaps the most familiar one, is the lever. A seesaw is a familiar example of a lever, with two people sitting on either end of a board and a pivoting point in the middle. There are three basic parts in all levers. They are the fulcrum “F,” a force or effort “E,” and a resistance “R.” Shown in Figure 1 are the pivot point “F” (fulcrum), the effort “E” which is applied at a distance “L” from the fulcrum, and a resistance “R” which acts at a distance “l” from the fulcrum. Distances “L” and “l” are the lever arms.The concept of torque was discussed earlier and torque is very much involved in the operation of a lever. When a person sits on one end of a seesaw, that person applies a downward force in pounds which acts along the distance to the center of the seesaw. This combination of force and distance creates torque, which tries to cause rotation.
First Class Lever
In the first class lever, the fulcrum is located between the effort and the resistance. As mentioned earlier, the seesaw is a good example of a lever, and it happens to be a first class lever. The amount of weight and the distance from the fulcrum can be varied to suit the need. Increasing the distance from the applied effort to the fulcrum, compared to the distance from the fulcrum to the weight being moved, increases the advantage provided by the lever. Crowbars, shears, and pliers are common examples of this class of lever. The proper balance of an airplane is also a good example, with the center of lift on the wing being the pivot point, or fulcrum, and the weight fore and aft of this point being the effort and the resistance.When calculating how much effort is required to lift a specific weight, or how much weight can be lifted by a specific effort, the following formula can be used.
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l) What this formula really shows is the input torque (effort × effort arm) equals the output torque (resistance × resistance arm). This formula and concept apply to all three classes of levers and to all simple machines in general.
Example: A first class lever is to be used to lift a 500-lb weight. The distance from the weight to the fulcrum is 12 inches and from the fulcrum to the applied effort is 60 inches. How much force is required to lift the weight?
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l)
E × 60 in = 500 lb × 12 in
E = 500 lb × 12 in ÷ 60 in
E = 100 lb
The mechanical advantage of the lever in this example would be:
Mechanical Advantage = Force Out ÷ Force In
= 500 lb ÷ 100 lb
= 5, or 5 to 1
An interesting thing to note with this example lever is if the applied effort moved down 10 inches, the weight on the other end would only move up 2 inches. The weight being lifted would only move one-fifth as far. The reason for this is the concept of work. If it allows you to lift 5 times more weight, you will only move it 1⁄5 as far as you move the effort, because a lever cannot have more work output than input.
Second Class Lever
The second class lever has the fulcrum at one end and the effort is applied at the other end. The resistance is somewhere between these points. A wheelbarrow is a good example of a second class lever, with the wheel at one end being the fulcrum, the handles at the opposite end being the applied effort, and the bucket in the middle being where the weight or resistance is placed. [Figure 2]Both first and second class levers are commonly used to help in overcoming big resistances with a relatively small effort. The first class lever, however, is more versatile. Depending on how close or how far away the weight is placed from the fulcrum, the first class lever can be made to gain force or gain distance, but not both at the same time. The second class lever can only be made to gain force.
Example: The distance from the center of the wheel to the handles on a wheelbarrow is 60 inches. The weight in the bucket is 18 inches from the center of the wheel. If 300 lb is placed in the bucket, how much force must be applied at the handles to lift the wheelbarrow?
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l)
E × 60 inches = 300 lb × 18 in
E = 300 lb × 18 in ÷ 60 in
E = 90 lb
The mechanical advantage of the lever in this example would be:
Mechanical Advantage = Force Out ÷ Force In
= 300 lb ÷ 90 lb
= 3.33, or 3.33 to 1
Example: The distance from the center of the wheel to the handles on a wheelbarrow is 60 inches. The weight in the bucket is 18 inches from the center of the wheel. If 300 lb is placed in the bucket, how much force must be applied at the handles to lift the wheelbarrow?
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l)
E × 60 inches = 300 lb × 18 in
E = 300 lb × 18 in ÷ 60 in
E = 90 lb
The mechanical advantage of the lever in this example would be:
Mechanical Advantage = Force Out ÷ Force In
= 300 lb ÷ 90 lb
= 3.33, or 3.33 to 1
Third Class Lever
There are occasions when it is desirable to speed up the movement of the resistance even though a large amount of effort must be used. Levers that help accomplish this are third class levers. As shown in Figure 3, the fulcrum is at one end of the lever and the weight or resistance to be overcome is at the other end, with the effort applied at some point between. Third class levers are easily recognized because the effort is applied between the fulcrum and the resistance. The retractable main landing gear on an airplane is a good example of a third class lever. The top of the landing gear, where it attaches to the airplane, is the pivot point. The wheel and brake assembly at the bottom of the landing gear is the resistance. The hydraulic actuator that makes the gear retract is attached somewhere in the middle, and that is the applied effort.The Pulley
Pulleys are simple machines in the form of a wheel mounted on a fixed axis and supported by a frame. The wheel, or disk, is normally grooved to accommodate a rope. The wheel is sometimes referred to as a “sheave,” or sometimes “sheaf.” The frame that supports the wheel is called a block. A block and tackle consists of a pair of blocks. Each block contains one or more pulleys and a rope connecting the pulley(s) of each block.Single Fixed Pulley
A single fixed pulley is really a first class lever with equal arms. In Figure 4, the arm from point “R” to point “F” is equal to the arm from point “F” to point “E,” with both distances being equal to the radius of the pulley. When a first class lever has equal arms, the mechanical advantage is 1. Thus, the force of the pull on the rope must be equal to the weight of the object being lifted. The only advantage of a single fixed pulley is to change the direction of the force, or pull on the rope.Single Movable Pulley
A single pulley can be used to magnify the force exerted. In Figure 5, the pulley is movable, and both ropes extending up from the pulley are sharing in the support of the weight. This single, movable pulley will act like a second class lever. The effort arm (EF) being the diameter of this pulley and the resistance arm (FR) being the radius of this pulley. This type of pulley would have a mechanical advantage of two because the diameter of the pulley is double the radius of the pulley. In use, if someone pulled in 4 ft of the effort rope, the weight would only rise off the floor 2 ft. If the weight was 100 lb, the effort applied would only need to be 50 lb. With this type of pulley, the effort will always be one-half of the weight being lifted.Block and Tackle
A block and tackle is made up of multiple pulleys, some of them fixed and some movable. In Figure 6, the block and tackle is made up of four pulleys, the top two being fixed and the bottom two being movable. Viewing the figure from right to left, notice there are four ropes supporting the weight and a fifth rope where the effort is applied. The number of weight supporting ropes determines the mechanical advantage of a block and tackle, so in this case the mechanical advantage is four. If the weight was 200 lb, it would require a 50 lb effort to lift it.The Gear
Two gears with teeth on their outer edges, as shown in Figure 7, act like a first class lever when one gear drives the other. The gear with the input force is called the drive gear, and the other is called the driven gear. The effort arm is the diameter of the driven gear, and the resistance arm is the diameter of the drive gear.Notice that the two gears turn in opposite directions: the bottom one clockwise and the top one counterclockwise. The gear on top is 9 inches in diameter and has 45 teeth, and the gear on the bottom is 12 inches in diameter and has 60 teeth.
Imagine that the blue gear is driving the yellow one, which makes the blue the drive and the yellow the driven. The mechanical advantage in terms of force would be the effort arm divided by the resistance arm, or 9 ÷ 12, which is 0.75. This would actually be called a fractional disadvantage, because there would be less force out than force in. The mechanical advantage in terms of distance, in rpm in this case, would be 12 ÷ 9, or 1.33.
Imagine that the blue gear is driving the yellow one, which makes the blue the drive and the yellow the driven. The mechanical advantage in terms of force would be the effort arm divided by the resistance arm, or 9 ÷ 12, which is 0.75. This would actually be called a fractional disadvantage, because there would be less force out than force in. The mechanical advantage in terms of distance, in rpm in this case, would be 12 ÷ 9, or 1.33.
This analysis tells us that when a large gear drives a small one, the small one turns faster and has less available force. In order to be a force gaining machine, the small gear needs to turn the large one. When the terminology reduction gearbox is used, such as a propeller reduction gearbox, it means that there is more rpm going in than is coming out. The end result is an increase in force, and ultimately torque.
Bevel gears are used to change the plane of rotation, so that a shaft turning horizontally can make a vertical shaft rotate. The size of the gears and their number of teeth determine the mechanical advantage, and whether force is being increased or rpm is being increased. If each gear has the same number of teeth, there would be no change in force or rpm. [Figure 8]
Bevel gears are used to change the plane of rotation, so that a shaft turning horizontally can make a vertical shaft rotate. The size of the gears and their number of teeth determine the mechanical advantage, and whether force is being increased or rpm is being increased. If each gear has the same number of teeth, there would be no change in force or rpm. [Figure 8]
The worm gear has an extremely high mechanical advantage. The input force goes into the spiral worm gear, which drives the spur gear. One complete revolution of the worm gear only makes the spur gear move an amount equal to one tooth. The mechanical advantage is equal to the number of teeth on the spur gear, which in this case there are 25. This is a force gaining machine, to the tune of 25 times more output force. [Figure 9]
The planetary sun gear system is typical of what would be found in a propeller reduction gearbox. The power output shaft of the engine would drive the sun gear in the middle, which rotates the planetary gears and ultimately the ring gear. In this example, the sun gear has 28 teeth, each planet gear has 22 teeth, and the ring gear has 82 teeth. To figure how much gear reduction is taking place, the number of teeth on the ring gear is divided by the number of teeth on the sun gear. In this case, the gear reduction is 2.93, meaning the engine has an rpm 2.93 times greater than the propeller. [Figure 10]
Inclined Plane
The inclined plane is a simple machine that facilitates the raising or lowering of heavy objects by application of a small force over a relatively long distance. Some familiar examples of the inclined plane are mountain highways and a loading ramp on the back of a moving truck. When weighing a small airplane, like a Cessna 172, an inclined plane, or ramp, can be used to get the airplane on the scales by pushing it, rather than jacking it. A ramp can be seen in Figure 11, where a Cessna 172 right main gear is sitting on an electronic scale. The airplane was pushed up the ramps to get it on the scales.With an inclined plane, the length of the incline is the effort arm and the vertical height of the incline is the resistance arm. If the length of the incline is five times greater than the height, there will be a force advantage, or mechanical advantage, of five. The Mooney M20 in Figure 11 weighed 1,600 lb on the day of the weighting. The ramp it is sitting on is 6 inches tall, which is the resistance arm, and the length of the ramp is 24 inches, which is the effort arm. To calculate the force needed to push the airplane up the ramps, use the same formula introduced earlier when levers were discussed, as follows:
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l)
E × 24 in = 1,600 lb × 6 in
E = 1,600 l-b × 6 in ÷ 24 in
E = 400 lb
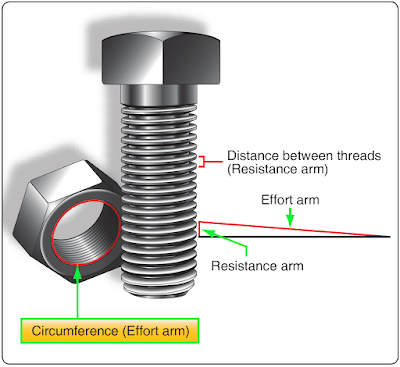
Bolts, screws, and wedges are also examples of devices that operate on the principle of the inclined plane. A bolt, for example, has a spiral thread that runs around its circumference. As the thread winds around the bolt’s circumference, it moves a vertical distance equal to the space between the threads. The circumference of the bolt is the effort arm and the distance between the threads is the resistance arm. [Figure 12] Based on this analysis, a fine threaded bolt, which has more threads per inch, has a greater mechanical advantage than a coarse threaded bolt.
Effort (E) × Effort Arm (L) = Resistance (R) × Resistance Arm (l)
E × 24 in = 1,600 lb × 6 in
E = 1,600 l-b × 6 in ÷ 24 in
E = 400 lb
Bolts, screws, and wedges are also examples of devices that operate on the principle of the inclined plane. A bolt, for example, has a spiral thread that runs around its circumference. As the thread winds around the bolt’s circumference, it moves a vertical distance equal to the space between the threads. The circumference of the bolt is the effort arm and the distance between the threads is the resistance arm. [Figure 12] Based on this analysis, a fine threaded bolt, which has more threads per inch, has a greater mechanical advantage than a coarse threaded bolt.
A chisel is a good example of a wedge. A chisel might be 8 inches long and only 1⁄2 inch wide, with a sharp tip and tapered sides. The 8-inch length is the effort arm and the 1⁄2 inch width is the resistance arm. This chisel would provide a force advantage, or mechanical advantage, of 16.
RELATED POSTS
RELATED POSTS