Force
Before the concept of work, power, or torque can be discussed, we need to understand what force means. According to the dictionary, force is the intensity of an impetus, or the intensity of an input. For example, if we apply a force to an object, the tendency will be for the object to move. Another way to look at it is that for work, power, or torque to exist, there must be a force that initiates the process.The unit for force in the English system of measurement is pounds, and in the metric system it is newtons. One pound of force is equal to 4.448 newtons. When we calculate the thrust of a turbine engine, we use the formula “Force = Mass × Acceleration,” and the thrust of the engine is expressed in pounds. The GE90-115 turbofan engine (power plant for the Boeing 777-300), for example, has 115,000 pounds of thrust.
Work
The study of machines, both simple and complex, can be seen as a study of the energy of mechanical work. This is true because all machines transfer input energy, or the work done on the machine, to output energy, or the work done by the machine.Work, in the mechanical sense of the term, is done when a resistance is overcome by force acting through a measurable distance. Two factors are involved: (1) force and (2) movement through a distance. As an example, suppose a small aircraft is stuck in the snow. Two men push against it for a period of time, but the aircraft does not move. According to the technical definition, no work had been done when the men were pushing against the aircraft. By definition, work is accomplished only when an object is displaced some distance against a resistive force. To calculate work, the following formula is used:
Work = Force (F) × distance (d)
In the English system, the force will be identified in pounds and the distance either in feet or inches, so the units will be foot-pounds or inch-pounds. Notice these are the same units that were used for potential and kinetic energy.
In the metric system, the force is identified in newtons (N) and the distance in meters, with the resultant units being joules. One pound of force is equal to 4.448 N and one meter is equal to 3.28 feet. One joule is equal to 1.36 ft-lb.
Example: How much work is accomplished by jacking a 150,000-lb Airbus A-320 airplane a vertical height of 4 ft? [Figure 1]
F = kF'
For example, if the coefficient of sliding friction of a smooth iron block on a smooth, horizontal surface is 0.3, the force required to start a 10 lb block would be 3 lb; a 40-lb block, 12 lb.
Starting friction for objects equipped with wheels and roller bearings is much smaller than that for sliding objects. For example, a locomotive would have difficulty getting a long train of cars in motion all at one time. Therefore, the couples between the cars are purposely made to have a few inches of play. When starting the train, the engineer backs the engine until all the cars are pushed together. Then, with a quick start forward the first car is set in motion. This technique is employed to overcome the static friction of each wheel as well as the inertia of each car. It would be impossible for the engine to start all of the cars at the same instant, for static friction, which is the resistance of being set in motion, would be greater than the force exerted by the engine. However, once the cars are in motion, the static friction is greatly reduced and a smaller force is required to keep the train in motion than was required to start it.
F = mN
In the formula above, “F” is the resistive force due to friction expressed in pounds; “N” is the force exerted on or by the object perpendicular (normal) to the surface over which it slides; and “m” (mu) is the coefficient of sliding friction. On a horizontal surface, N is equal to the weight of the object in pounds. The area of the sliding object exposed to the sliding surface has no effect on the results. A block of wood, for example, will not slide any easier on one of the broad sides than it will on a narrow side, assuming all sides have the same smoothness. Therefore, area does not enter into the equation above.
Example: An aircraft with a gross weight of 79,600 lb is towed over a concrete ramp. What force must be exerted by the towing vehicle to keep the airplane rolling after once set in motion?
F = mN
= 0.02 mu × 79,600 lb
= 1,592 lb
Power = Force × distance ÷ time
The units for power will be foot-pounds per minute, foot-pounds per second, inch-pounds per minute or second, and possibly mile-pounds per hour. The units depend on how distance and time are measured.
Many years ago, there was a desire to compare the power of the newly evolving steam engine to that of horses. People wanted to know how many horses the steam engine was equivalent to. The value we know currently as one horsepower (hp) was developed, and it is equal to 550 foot-pounds per second (ft-lb/s) because of this. It was found that the average horse could lift a weight of 550 lb, one foot off the ground, in one second. The values we use today, in order to convert power to horsepower, are as follows:
1 hp = 550 ft-lb/s
1 hp = 33,000 ft-lb/min.
1 hp = 375 mile pounds per hour (mi-lb/hr.)
1 hp = 746 watts (electricity conversion)
To convert power to horsepower, divide the power by the appropriate conversion based on the units being used.
Example: What power would be needed, and also horsepower, to raise the GE-90 turbofan engine into position to install it on a Boeing 777-300 airplane? The engine weighs 19,000 lb, and it must be lifted 4 ft in 2 minutes.
Power = Force × distance ÷ time
= 19,000 lb × 4 ft ÷ 2 min.
= 38,000 ft-lb/min.
Hp = 38,000 ft-lb/min. ÷ 33,000 ft-lb/min.
Hp = 1.15
The hoist that will be used to raise this engine into position will need to be powered by an electric motor because the average person will not be able to generate 1.15 hp in their arms for the necessary 2 minutes.
If we push on an object with a force of 10 lb and it moves 10 inches in a straight line, we have done 100 in-lb of work. By comparison, if we have a wrench 10 inches long that is on a bolt, and we push down on it with a force of 10 lb, a torque of 100 lb-in is applied to the bolt. If the bolt was already tight and did not move as we pushed down on the wrench, the torque of 100 lb-in would still exist. The formula for torque is:
Torque = Force × distance
Even though this formula looks the same as the other formula for calculating work, recognize that the distance value in this formula is not the linear distance an object moves, but rather the distance along which the force is applied.
Notice that with torque nothing had to move, because the force is being applied along a distance and not through a distance. Notice also that although the units of work and torque appear to be the same, they are not. The units of work were inch-pounds and the units of torque were pound-inches, and that is what differentiates the two.
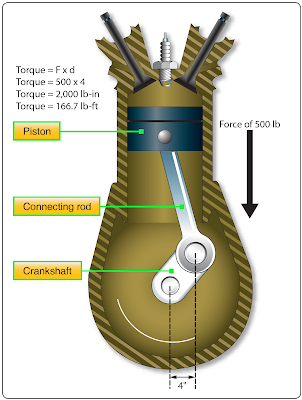
Torque is very important when thinking about how engines work, both piston engines and gas turbine engines. Both types of engines create torque in advance of being able to create work or power. With a piston engine, a force in pounds pushes down on the top of the piston and tries to make it move. The piston is attached to the connecting rod, which is attached to the crankshaft at an offset. That offset would be like the length of the wrench discussed earlier, and the force acting along that length is what creates torque. [Figure 3]
Example: How much work is accomplished by jacking a 150,000-lb Airbus A-320 airplane a vertical height of 4 ft? [Figure 1]
Work = Force × Distance
= 150,000 lb × 4 ft
= 600,000 ft-lb
Example: How much work is accomplished when a tow tractor is hooked up to a tow bar and a Boeing 737-800 airplane weighing 130,000 lb is pushed 80 ft. into the hangar? The force on the tow bar is 5,000 lb.
Work = Force × Distance
= 5,000 lb × 80 ft
= 400,000 ft-lb
In this last example, notice the force does not equal the weight of the airplane. This is because the airplane is being moved horizontally and not lifted vertically. In almost all cases, it takes less work to move something horizontally than it does to lift it vertically. Most people can push their car a short distance if it runs out of gas, but they cannot get under their car and lift it off the ground.
= 150,000 lb × 4 ft
= 600,000 ft-lb
Example: How much work is accomplished when a tow tractor is hooked up to a tow bar and a Boeing 737-800 airplane weighing 130,000 lb is pushed 80 ft. into the hangar? The force on the tow bar is 5,000 lb.
Work = Force × Distance
= 5,000 lb × 80 ft
= 400,000 ft-lb
In this last example, notice the force does not equal the weight of the airplane. This is because the airplane is being moved horizontally and not lifted vertically. In almost all cases, it takes less work to move something horizontally than it does to lift it vertically. Most people can push their car a short distance if it runs out of gas, but they cannot get under their car and lift it off the ground.
Friction and Work
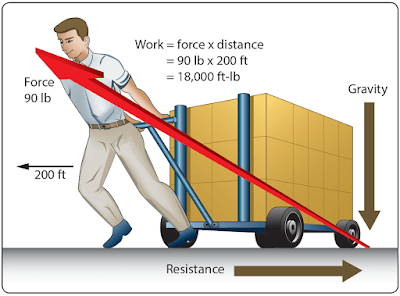
In calculating work done, the actual resistance overcome is measured. This is not necessarily the weight of the object being moved. [Figure 2] A 900-lb load is being pulled a distance of 200 ft. This does not mean that the work done (force × distance) is 180,000 ft-lb (900 lb × 200 ft). This is because the person pulling the load is not working against the total weight of the load, but rather against the rolling friction of the cart, which may be no more than 90 lb.Friction is an important aspect of work. Without friction, it would be impossible to walk. One would have to shove oneself from place to place, and would have to bump against some obstacle to stop at a destination. Yet friction is a liability as well as an asset, and requires consideration when dealing with any moving mechanism.
In experiments relating to friction, measurement of the applied forces reveals that there are three kinds of friction. One force is required to start a body moving, while another is required to keep the body moving at constant speed. Also, after a body is in motion, a definitely larger force is required to keep it sliding than to keep it rolling.
Thus, the three kinds of friction may be classified as: (1) starting or static friction, (2) sliding friction, and (3) rolling friction.
In experiments relating to friction, measurement of the applied forces reveals that there are three kinds of friction. One force is required to start a body moving, while another is required to keep the body moving at constant speed. Also, after a body is in motion, a definitely larger force is required to keep it sliding than to keep it rolling.
Thus, the three kinds of friction may be classified as: (1) starting or static friction, (2) sliding friction, and (3) rolling friction.
Static Friction
When an attempt is made to slide a heavy object along a surface, the object must first be broken loose or started. Once in motion, it slides more easily. The “breaking loose” force is, of course, proportional to the weight of the body. The force necessary to start the body moving slowly is designated “F,” and “F'” is the normal force pressing the body against the surface which is usually its weight. Since the nature of the surfaces rubbing against each other is important, they must be considered. The nature of the surfaces is indicated by the coefficient of starting friction which is designated by the letter “k.” This coefficient can be established for various materials and is often published in tabular form. Thus, when the load (weight of the object) is known, starting friction can be calculated by using the following formula:F = kF'
For example, if the coefficient of sliding friction of a smooth iron block on a smooth, horizontal surface is 0.3, the force required to start a 10 lb block would be 3 lb; a 40-lb block, 12 lb.
Starting friction for objects equipped with wheels and roller bearings is much smaller than that for sliding objects. For example, a locomotive would have difficulty getting a long train of cars in motion all at one time. Therefore, the couples between the cars are purposely made to have a few inches of play. When starting the train, the engineer backs the engine until all the cars are pushed together. Then, with a quick start forward the first car is set in motion. This technique is employed to overcome the static friction of each wheel as well as the inertia of each car. It would be impossible for the engine to start all of the cars at the same instant, for static friction, which is the resistance of being set in motion, would be greater than the force exerted by the engine. However, once the cars are in motion, the static friction is greatly reduced and a smaller force is required to keep the train in motion than was required to start it.
Sliding Friction
Sliding friction is the resistance to motion offered by an object sliding over a surface. It pertains to friction produced after the object has been set in motion, and is always less than starting friction. The amount of sliding resistance is dependent on the nature of the surface of the object, the surface over which it slides, and the normal force between the object and the surface. This resistive force may be computed by using the following formula:F = mN
In the formula above, “F” is the resistive force due to friction expressed in pounds; “N” is the force exerted on or by the object perpendicular (normal) to the surface over which it slides; and “m” (mu) is the coefficient of sliding friction. On a horizontal surface, N is equal to the weight of the object in pounds. The area of the sliding object exposed to the sliding surface has no effect on the results. A block of wood, for example, will not slide any easier on one of the broad sides than it will on a narrow side, assuming all sides have the same smoothness. Therefore, area does not enter into the equation above.
Rolling Friction
Resistance to motion is greatly reduced if an object is mounted on wheels or rollers. The force of friction for objects mounted on wheels or rollers is called rolling friction. This force may be computed by the same equation used in computing sliding friction, but the values of “m” will be much smaller. For example, the value of “m” for rubber tires on concrete or macadam is about 0.02. The value of “m” for roller bearings is very small, usually ranging from 0.001 to 0.003 and is often disregarded.Example: An aircraft with a gross weight of 79,600 lb is towed over a concrete ramp. What force must be exerted by the towing vehicle to keep the airplane rolling after once set in motion?
F = mN
= 0.02 mu × 79,600 lb
= 1,592 lb
Power
The concept of power involves the previously discussed topic of work, which was a force being applied over a measured distance, but adds one more consideration—time. In other words, how long it takes to accomplish the work. If someone asked the average person if he or she could lift one million pounds 5 feet off the ground, the answer most assuredly would be no. This person would probably assume that he or she is to lift it all at once. What if he or she is given 365 days to lift it, and could lift small amounts of weight at a time? The work involved would be the same, regardless of how long it took to lift the weight, but the power required is different. If the weight is to be lifted in a shorter period of time, it will take more power. The formula for power is as follows:Power = Force × distance ÷ time
The units for power will be foot-pounds per minute, foot-pounds per second, inch-pounds per minute or second, and possibly mile-pounds per hour. The units depend on how distance and time are measured.
Many years ago, there was a desire to compare the power of the newly evolving steam engine to that of horses. People wanted to know how many horses the steam engine was equivalent to. The value we know currently as one horsepower (hp) was developed, and it is equal to 550 foot-pounds per second (ft-lb/s) because of this. It was found that the average horse could lift a weight of 550 lb, one foot off the ground, in one second. The values we use today, in order to convert power to horsepower, are as follows:
1 hp = 550 ft-lb/s
1 hp = 33,000 ft-lb/min.
1 hp = 375 mile pounds per hour (mi-lb/hr.)
1 hp = 746 watts (electricity conversion)
To convert power to horsepower, divide the power by the appropriate conversion based on the units being used.
Example: What power would be needed, and also horsepower, to raise the GE-90 turbofan engine into position to install it on a Boeing 777-300 airplane? The engine weighs 19,000 lb, and it must be lifted 4 ft in 2 minutes.
Power = Force × distance ÷ time
= 19,000 lb × 4 ft ÷ 2 min.
= 38,000 ft-lb/min.
Hp = 38,000 ft-lb/min. ÷ 33,000 ft-lb/min.
Hp = 1.15
The hoist that will be used to raise this engine into position will need to be powered by an electric motor because the average person will not be able to generate 1.15 hp in their arms for the necessary 2 minutes.
Torque
Torque is a very interesting concept and occurrence, and it is definitely something that needs to be discussed in conjunction with work and power. Whereas work is described as force acting through a distance, torque is described as force acting along a distance. Torque is something that creates twisting and tries to make something rotate.If we push on an object with a force of 10 lb and it moves 10 inches in a straight line, we have done 100 in-lb of work. By comparison, if we have a wrench 10 inches long that is on a bolt, and we push down on it with a force of 10 lb, a torque of 100 lb-in is applied to the bolt. If the bolt was already tight and did not move as we pushed down on the wrench, the torque of 100 lb-in would still exist. The formula for torque is:
Torque = Force × distance
Even though this formula looks the same as the other formula for calculating work, recognize that the distance value in this formula is not the linear distance an object moves, but rather the distance along which the force is applied.
Notice that with torque nothing had to move, because the force is being applied along a distance and not through a distance. Notice also that although the units of work and torque appear to be the same, they are not. The units of work were inch-pounds and the units of torque were pound-inches, and that is what differentiates the two.
Torque is very important when thinking about how engines work, both piston engines and gas turbine engines. Both types of engines create torque in advance of being able to create work or power. With a piston engine, a force in pounds pushes down on the top of the piston and tries to make it move. The piston is attached to the connecting rod, which is attached to the crankshaft at an offset. That offset would be like the length of the wrench discussed earlier, and the force acting along that length is what creates torque. [Figure 3]
For the cylinder in Figure 3, there is a force of 500 lb pushing down on the top of the piston. The connecting rod attaches to the crankshaft at an offset distance of 4 in. The product of the force and the offset distance is the torque, in this case 2,000 lb-in.
In a turbine engine, the turbine blades at the back of the engine extract energy from the high velocity exhaust gases. The energy extracted becomes a force in pounds pushing on the turbine blades, which happen to be a certain number of inches from the center of the shaft they are trying to make rotate. The number of inches from the turbine blades to the center of the shaft would be like the length of the wrench discussed earlier.
Mathematically, there is a relationship between the horsepower of an engine and the torque of an engine. The formula that shows this relationship is as follows:
Torque = Horsepower × 5,252 ÷ rpm
Example: A Cessna 172R has a Lycoming IO-360 engine that creates 180 horsepower at 2,700 rpm. How many pound-feet of torque is the engine producing?
Torque = 180 × 5,252 ÷ 2,700
= 350 lb-ft.
RELATED POSTS
In a turbine engine, the turbine blades at the back of the engine extract energy from the high velocity exhaust gases. The energy extracted becomes a force in pounds pushing on the turbine blades, which happen to be a certain number of inches from the center of the shaft they are trying to make rotate. The number of inches from the turbine blades to the center of the shaft would be like the length of the wrench discussed earlier.
Mathematically, there is a relationship between the horsepower of an engine and the torque of an engine. The formula that shows this relationship is as follows:
Torque = Horsepower × 5,252 ÷ rpm
Example: A Cessna 172R has a Lycoming IO-360 engine that creates 180 horsepower at 2,700 rpm. How many pound-feet of torque is the engine producing?
Torque = 180 × 5,252 ÷ 2,700
= 350 lb-ft.
RELATED POSTS