Maintaining aircraft fuel systems in acceptable condition to deliver clean fuel to the engine(s) is a major safety factor in aviation. Personnel handling fuel or maintaining fuel systems should be properly trained and use best practices to ensure that the fuel, or fuel system, are not the cause of an incident or accident.
Keeping a fuel system clean begins with an awareness of the common types of contamination. Water is the most common. Solid particles, surfactants, and microorganisms are also common. However, contamination of fuel with another fuel not intended for use on a particular aircraft is possibly the worst type of contamination.
Checking for Fuel System Contaminants
Continuous vigilance is required when checking aircraft fuel systems for contaminants. Daily draining of strainers and sumps is combined with periodic filter changes and inspections to ensure fuel is contaminant free. Turbine powered engines have highly refined fuel control systems through which flow hundreds of pounds of fuel per hour of operation. Sumping alone is not sufficient. Particles are suspended longer in jet fuel due to its viscosity. Engineers design a series of filters into the fuel system to trap foreign matter. Technicians must supplement these with cautious procedures and thorough visual inspections to accomplish the overall goal of delivering clean fuel to the engines.Keeping a fuel system clean begins with an awareness of the common types of contamination. Water is the most common. Solid particles, surfactants, and microorganisms are also common. However, contamination of fuel with another fuel not intended for use on a particular aircraft is possibly the worst type of contamination.
Water contaminants
Water can be dissolved into fuel or entrained. Entrained water can be detected by a cloudy appearance to the fuel. Close examination is required. Air in the fuel tends to cause a similar cloudy condition but is near the top of the tank. The cloudiness caused by water in the fuel tends to be more towards the bottom of the tank as the water slowly settles out.As previously discussed, water can enter a fuel system via condensation. The water vapor in the vapor space above the liquid fuel in a fuel tank condenses when the temperature changes. It normally sinks to the bottom of the fuel tank into the sump where it can be drained off before flight. [Figure 1] However, time is required for this to happen. On some aircraft, a large amount of fuel needs to be drained before settled water reaches the drain valve. Awareness of this type of sump idiosyncrasy for a particular aircraft is important. The condition of the fuel and recent fueling practices need to be considered and are equally important. If the aircraft has been flown often and filled immediately after flight, there is little reason to suspect water contamination beyond what would be exposed during a routine sumping.An aircraft that has sat for a long period of time with partially full fuel tanks is a cause of concern.
It is possible that water is introduced into the aircraft fuel load during refueling with fuel that already contains water. Any suspected contamination from refueling or the general handling of the aircraft should be investigated. A change in fuel supplier may be required if water continues to be an issue despite efforts are made to keep the aircraft fuel tanks full and sumps drained on a regular basis. Note that fuel below freezing temperature may contain entrained water in ice form that may not settle into the sump until melted. Use of an anti-icing solution in turbine fuel tanks helps prevent filter blockage from water that condenses out of the fuel as ice during flight.
Strainers and filters are designed with upward flow exits to have water collect at the bottom of the fuel bowl to be drained off. This should not be overlooked. Entrained water in small quantities that makes it to the engine usually poses no problem. Large amounts of water can disrupt engine operation. Settled water in tanks can cause corrosion. This can be magnified by microorganisms that live in the fuel/water interface. High quantities of water in the fuel can also cause discrepancies in fuel quantity probe indications.
Preventing solid contaminant introduction into the fuel is critical. Whenever the fuel system is open, care must be taken to keep out foreign matter. Lines should be capped immediately. Fuel tank caps should not be left open for any longer than required to refuel the tanks. Clean the area adjacent to wherever the system is opened before it is opened. Coarse sediments are those visible to the naked eye. Should they pass beyond system filters, they can clog in fuel metering device orifices, sliding valves, and fuel nozzles. Fine sediments cannot actually be seen as individual particles. They may be detected as a haze in the fuel or they may refract light when examining the fuel. Their presence in fuel controls and metering devices is indicated by dark shellac-like marks on sliding surfaces.
The maximum amount of solid particle contamination allowable is much less in turbine engine fuel systems than in reciprocating-engine fuel systems. It is particularly important to regularly replace filter elements and investigate any unusual solid particles that collect therein. The discovery of significant metal particles in a filter could be a sign of a failing component upstream of the filter. A laboratory analysis is possible to determine the nature and possible source of solid contaminants.
Surfactants are usually in the fuel when it is introduced into the aircraft. Discovery of either excessive quantities of dirt and water making their way through the system or a sudsy residue in filters and sumps may indicate their presence. The source of fuel should be investigated and avoided if found to contain a high level of these chemicals. As mentioned, slow settling rates of solids and water into sumps is a key indicator that surfactant levels are high in the fuel. Most quality fuel providers have clay filter elements on their fuel dispensing trucks and in their fixed storage and dispensing systems.
These filters, if renewed at the proper intervals, remove most surfactants through adhesion. Surfactants discovered in the aircraft systems should be traced to the fuel supply source and the use and condition of these filters. [Figure 3]
Since the microbes live in free water and feed on fuel, the most powerful remedy for their presence is to keep water from accumulating in the fuel. Fuel 100 percent free of water is not practicable. By following best practices for sump draining and filter changes, combined with care of fuel stock tanks used to refuel aircraft, much of the potential for water to accumulate in the aircraft fuel tanks can be mitigated. The addition of biocides to the fuel when refueling also helps by killing organisms that are present.
If the wrong fuel is put into an aircraft, the situation must be rectified before flight. If discovered before the fuel pump is operated and an engine is started, drain all improperly filled tanks. Flush out the tanks and fuel lines with the correct fuel and then refill the tanks with the proper fuel. However, if discovered after an engine has been started or attempted to be started, the procedure is more in depth. The entire fuel system, including all fuel lines, components, metering device(s) and tanks, must be drained and flushed. If the engines have been operated, a compression test should be accomplished and the combustion chamber and pistons should be borescope inspected. Engine oil should be drained and all screens and filters examined for any evidence of damage. Once reassembled and the tanks have been filled with the correct fuel, a full engine run-up check should be performed before releasing the aircraft for flight.
Contaminated fuel caused by the introduction of small quantities of the wrong type of fuel into an aircraft may not look any different when visually inspected, making a dangerous situation more dangerous. Any person recognizing that this error has occurred must ground the aircraft. The lives of the aircraft occupants are at stake.
In addition to the detection methods mentioned for each type of contamination above, various field and laboratory tests can be performed on aircraft fuel to expose contamination. A common field test for water contamination is performed by adding a dye that dissolves in water but not fuel to a test sample drawn from the fuel tank. The more water present in the fuel, the greater the dye disperses and colors the sample.
Another common test kit commercially available contains a grey chemical powder that changes color to pink or purple when the contents of a fuel sample contains more than 30 parts per million (ppm) of water. A 15 ppm test is available for turbine engine fuel. [Figure 6] These levels of water are considered generally unacceptable and not safe for operation of the aircraft. If levels are discovered above these amounts, time for the water to settle out of the fuel should be given or the aircraft should be defueled and refueled with acceptable fuel.
The presence and level of microorganisms in a fuel tank can also be measured with a field device. The test detects the metabolic activity of bacteria, yeast, and molds, including sulfate reducing bacteria, and other anaerobe microorganisms. This could be used to determine the amount of anti-microbial agent to be added to the fuel. The testing unit is shown in Figure 7.
Bug test kits test fuel specifically for bacteria and fungus. While other types of microorganisms may exist, this semiquantitative test is quick and easy to perform. Treat a fuel sample with the product and match the color of the sample to the chart for an indication of the level of bacteria and fungus present. These are some of the most common types of microorganisms that grow in fuel; if growth levels of fungus and bacteria are acceptable, the fuel could be usable. [Figure 8]
Fuel trucks and fuel farms may make use of laser contaminant identification technology. All fuel exiting the storage tank going into the servicing hose is passed through the analyzer unit. Laser sensing technology determines the difference between water and solid particle contaminants. When an excessive level of either is detected, the unit automatically shuts off flow to the fueling nozzle. Thus, aircraft are fueled only with clean dry fuel. When surfactant filters are combined with contaminant identification technology and microorganism detection, chances of delivering clean fuel to the aircraft engines are good. [Figure 9]
Before various test kits were developed for use in the field by nonscientific personnel, laboratories provided complete fuel composition analysis to aviators. These services are still available. A sample is sent in a sterilized container to the lab. It can be tested for numerous factors including water, microbial growth, flash point, specific gravity, cetane index (a measure of combustibility and burning characteristics), and more. Tests for microbes involve growing cultures of whatever organisms are present in the fuel. [Figure 10]
Contamination control begins long before the fuel gets pumped into an aircraft fuel tank. Many standard petroleum industry safeguards are in place. Fuel farm and delivery truck fuel handling practices are designed to control contamination. Various filters, testing, and treatments effectively keep fuel contaminant free or remove various contaminants once discovered. However, the correct clean fuel for an aircraft should never be taken for granted. The condition of all storage tanks and fuel trucks should be monitored. All filter changes and treatments should occur regularly and on time. The fuel supplier should take pride in delivering clean, contaminant free fuel to its customers.
 |
| Figure 1. A sump drain tool used to open and collect fuel and contaminants from the fuel system sumps. Daily sump draining is part of the procedures needed to remove water from fuel that is to be delivered to the engine(s) |
It is possible that water is introduced into the aircraft fuel load during refueling with fuel that already contains water. Any suspected contamination from refueling or the general handling of the aircraft should be investigated. A change in fuel supplier may be required if water continues to be an issue despite efforts are made to keep the aircraft fuel tanks full and sumps drained on a regular basis. Note that fuel below freezing temperature may contain entrained water in ice form that may not settle into the sump until melted. Use of an anti-icing solution in turbine fuel tanks helps prevent filter blockage from water that condenses out of the fuel as ice during flight.
Note that the fuel anti-ice additive level should be monitored so that recommended quantity for the tank capacity is maintained. After repeated fueling, the level can be obscured. A field hand-held test unit can be used to check the amount of anti-ice additive already in a fuel load. [Figure 2]
 |
| Figure 2. A hand-held refractometer with digital display measures the amount of fuel anti-ice additive contained in a fuel load |
Strainers and filters are designed with upward flow exits to have water collect at the bottom of the fuel bowl to be drained off. This should not be overlooked. Entrained water in small quantities that makes it to the engine usually poses no problem. Large amounts of water can disrupt engine operation. Settled water in tanks can cause corrosion. This can be magnified by microorganisms that live in the fuel/water interface. High quantities of water in the fuel can also cause discrepancies in fuel quantity probe indications.
Solid Particle Contaminants
Solid particles that do not dissolve in the fuel are common contaminants. Dirt, rust, dust, metal particles, and just about anything that can find its way into an open fuel tank is of concern. Filter elements are designed to trap these contaminants and some fall into the sump to be drained off. Pieces of debris from the inside of the fuel system may also accumulate, such as broken-off sealant, or pieces of filter elements, corrosion, etc.Preventing solid contaminant introduction into the fuel is critical. Whenever the fuel system is open, care must be taken to keep out foreign matter. Lines should be capped immediately. Fuel tank caps should not be left open for any longer than required to refuel the tanks. Clean the area adjacent to wherever the system is opened before it is opened. Coarse sediments are those visible to the naked eye. Should they pass beyond system filters, they can clog in fuel metering device orifices, sliding valves, and fuel nozzles. Fine sediments cannot actually be seen as individual particles. They may be detected as a haze in the fuel or they may refract light when examining the fuel. Their presence in fuel controls and metering devices is indicated by dark shellac-like marks on sliding surfaces.
The maximum amount of solid particle contamination allowable is much less in turbine engine fuel systems than in reciprocating-engine fuel systems. It is particularly important to regularly replace filter elements and investigate any unusual solid particles that collect therein. The discovery of significant metal particles in a filter could be a sign of a failing component upstream of the filter. A laboratory analysis is possible to determine the nature and possible source of solid contaminants.
Surfactants
Surfactants are liquid chemical contaminants that naturally occur in fuels. They can also be introduced during the refining or handling processes. These surface active agents usually appear as tan to dark brown liquid when they are present in large quantities. They may even have a soapy consistency. Surfactants in small quantities are unavoidable and pose little threat to fuel system functioning. Larger quantities of surfactants do pose problems. In particular, they reduce the surface tension between water and the fuel and tend to cause water and even small particles in the fuel to remain suspended rather than settling into the sumps. Surfactants also tend to collect in filter elements making them less effective.Surfactants are usually in the fuel when it is introduced into the aircraft. Discovery of either excessive quantities of dirt and water making their way through the system or a sudsy residue in filters and sumps may indicate their presence. The source of fuel should be investigated and avoided if found to contain a high level of these chemicals. As mentioned, slow settling rates of solids and water into sumps is a key indicator that surfactant levels are high in the fuel. Most quality fuel providers have clay filter elements on their fuel dispensing trucks and in their fixed storage and dispensing systems.
These filters, if renewed at the proper intervals, remove most surfactants through adhesion. Surfactants discovered in the aircraft systems should be traced to the fuel supply source and the use and condition of these filters. [Figure 3]
 |
| Figure 3. Clay filter elements remove surfactants. They are used in the fuel dispensing system before fuel enters the aircraft |
Microorganisms
The presence of microorganisms in turbine engine fuels is a critical problem. There are hundreds of varieties of these life forms that live in free water at the junction of the water and fuel in a fuel tank. They form a visible slime that is dark brown, grey, red, or black in color. This microbial growth can multiply rapidly and can cause interference with the proper functioning of filter elements and fuel quantity indicators. Moreover, the slimy water/microbe layer in contact with the fuel tank surface provides a medium for electrolytic corrosion of the tank. [Figure 4] |
| Figure 4. This fuel-water sample has microbial growth at the interface of the two liquids |
Since the microbes live in free water and feed on fuel, the most powerful remedy for their presence is to keep water from accumulating in the fuel. Fuel 100 percent free of water is not practicable. By following best practices for sump draining and filter changes, combined with care of fuel stock tanks used to refuel aircraft, much of the potential for water to accumulate in the aircraft fuel tanks can be mitigated. The addition of biocides to the fuel when refueling also helps by killing organisms that are present.
Foreign Fuel Contamination
Aircraft engines operate effectively only with the proper fuel. Contamination of an aircraft’s fuel with fuel not intended for use in that particular aircraft can have disastrous consequences. It is the responsibility of all aviators to put forth effort continuously to ensure that only the fuel designed for the operation of the aircraft’s engine(s) is put into the fuel tanks. Each fuel tank receptacle or fuel cap area is clearly marked to indicate which fuel is required. [Figure 5] |
| Figure 5. All entry points of fuel into the aircraft are marked with the type of fuel to be used. Never introduce any other fuel into the aircraft other than that which is specified |
If the wrong fuel is put into an aircraft, the situation must be rectified before flight. If discovered before the fuel pump is operated and an engine is started, drain all improperly filled tanks. Flush out the tanks and fuel lines with the correct fuel and then refill the tanks with the proper fuel. However, if discovered after an engine has been started or attempted to be started, the procedure is more in depth. The entire fuel system, including all fuel lines, components, metering device(s) and tanks, must be drained and flushed. If the engines have been operated, a compression test should be accomplished and the combustion chamber and pistons should be borescope inspected. Engine oil should be drained and all screens and filters examined for any evidence of damage. Once reassembled and the tanks have been filled with the correct fuel, a full engine run-up check should be performed before releasing the aircraft for flight.
Contaminated fuel caused by the introduction of small quantities of the wrong type of fuel into an aircraft may not look any different when visually inspected, making a dangerous situation more dangerous. Any person recognizing that this error has occurred must ground the aircraft. The lives of the aircraft occupants are at stake.
Detection of Contaminants
Visual inspection of fuel should always reveal a clean, bright looking liquid. Fuel should not be opaque, which could be a sign of contamination and demands further investigation. As mentioned, the technician must always be aware of the fuel’s appearance, as well as when and from what sources refueling has taken place. Any suspicion of contamination must be investigated.In addition to the detection methods mentioned for each type of contamination above, various field and laboratory tests can be performed on aircraft fuel to expose contamination. A common field test for water contamination is performed by adding a dye that dissolves in water but not fuel to a test sample drawn from the fuel tank. The more water present in the fuel, the greater the dye disperses and colors the sample.
Another common test kit commercially available contains a grey chemical powder that changes color to pink or purple when the contents of a fuel sample contains more than 30 parts per million (ppm) of water. A 15 ppm test is available for turbine engine fuel. [Figure 6] These levels of water are considered generally unacceptable and not safe for operation of the aircraft. If levels are discovered above these amounts, time for the water to settle out of the fuel should be given or the aircraft should be defueled and refueled with acceptable fuel.
 |
| Figure 6. This kit allows periodic testing for water in fuel |
The presence and level of microorganisms in a fuel tank can also be measured with a field device. The test detects the metabolic activity of bacteria, yeast, and molds, including sulfate reducing bacteria, and other anaerobe microorganisms. This could be used to determine the amount of anti-microbial agent to be added to the fuel. The testing unit is shown in Figure 7.
 |
| Figure 7. A capture solution is put into a 1 liter sample of fuel and shaken. The solution is then put into the analyzer shown to determine the level of microorganisms in the fuel |
Bug test kits test fuel specifically for bacteria and fungus. While other types of microorganisms may exist, this semiquantitative test is quick and easy to perform. Treat a fuel sample with the product and match the color of the sample to the chart for an indication of the level of bacteria and fungus present. These are some of the most common types of microorganisms that grow in fuel; if growth levels of fungus and bacteria are acceptable, the fuel could be usable. [Figure 8]
 |
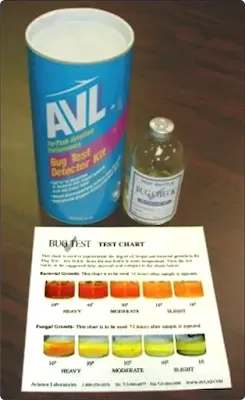| Figure 8. Fuel bug test kits identify the level of bacteria and fungus present in a fuel load by comparing the color of a treated sample with a color chart |
Fuel trucks and fuel farms may make use of laser contaminant identification technology. All fuel exiting the storage tank going into the servicing hose is passed through the analyzer unit. Laser sensing technology determines the difference between water and solid particle contaminants. When an excessive level of either is detected, the unit automatically shuts off flow to the fueling nozzle. Thus, aircraft are fueled only with clean dry fuel. When surfactant filters are combined with contaminant identification technology and microorganism detection, chances of delivering clean fuel to the aircraft engines are good. [Figure 9]
 |
| Figure 9. This contaminant analyzer is used on fuel supply source outflow, such as that on a refueling truck. Water and solid contaminant levels are detected using laser identification technology. The valve to the fill hose is automatically closed when levels of either are elevated beyond acceptable limits |
Before various test kits were developed for use in the field by nonscientific personnel, laboratories provided complete fuel composition analysis to aviators. These services are still available. A sample is sent in a sterilized container to the lab. It can be tested for numerous factors including water, microbial growth, flash point, specific gravity, cetane index (a measure of combustibility and burning characteristics), and more. Tests for microbes involve growing cultures of whatever organisms are present in the fuel. [Figure 10]
 |
| Figure 10. Laboratory tests of fuel samples are available |
Fuel Contamination Control
A continuous effort must be put forth by all those in the aviation industry to ensure that each aircraft is fueled only with clean fuel of the correct type. Many contaminants, both soluble and insoluble, can contaminate an aircraft’s fuel supply. They can be introduced with the fuel during fueling or the contamination may occur after the fuel is onboard.Contamination control begins long before the fuel gets pumped into an aircraft fuel tank. Many standard petroleum industry safeguards are in place. Fuel farm and delivery truck fuel handling practices are designed to control contamination. Various filters, testing, and treatments effectively keep fuel contaminant free or remove various contaminants once discovered. However, the correct clean fuel for an aircraft should never be taken for granted. The condition of all storage tanks and fuel trucks should be monitored. All filter changes and treatments should occur regularly and on time. The fuel supplier should take pride in delivering clean, contaminant free fuel to its customers.
Onboard aircraft fuel systems must be maintained and serviced according to manufacturer’s specifications. Samples from all drains should be taken and inspected on a regular basis. Filters should be changed at the specified intervals. The fuel load should be visually inspected and tested from time to time or when there is a potential contamination issue. Particles discovered in filters should be indentified and investigated if needed. Inspection of the fuel system during periodic inspections should be treated with highest concern.
Most importantly, the choice of the correct fuel for an aircraft should never be in question. No one should ever put a fuel into an aircraft fuel tank unless absolutely certain it is the correct fuel for that aircraft and its engine(s). Personnel involved in fuel handling should be properly trained. All potential contamination situations should be investigated and remedied.
RELATED POSTS
Most importantly, the choice of the correct fuel for an aircraft should never be in question. No one should ever put a fuel into an aircraft fuel tank unless absolutely certain it is the correct fuel for that aircraft and its engine(s). Personnel involved in fuel handling should be properly trained. All potential contamination situations should be investigated and remedied.
RELATED POSTS