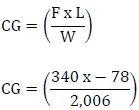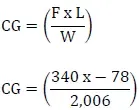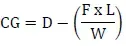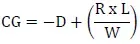Almost all weight and balance problems involve only simple math. This allows slide rules and hand-held electronic calculators to relieve much of the tedium involved with these problems. This post compares the methods of determining the center of gravity (CG) of an airplane while it is being weighed. First, it shows how to determine the CG using a simple electronic calculator, then solves the same problem using an E6-B flight computer. Finally, it shows how to solve it using a dedicated electronic flight computer Examples of typical weight and balance problems (solved with an electronic calculator) that pilots and airframe and powerplant (A&P) maintenance technicians encounter throughout their aviation endeavors are shown later in this post.
To determine the CG, use this formula:
Key the data into the calculator and press the equal (=) key. The answer should read as follows: (340)(×)(78)(+/–)(÷)(2006)(=) –13.2
The arm of the nosewheel is negative, so the CG is –13.2 or 13.2 inches ahead of the main wheel weighing points.
The same problem that was just solved with the electronic calculator can be solved on an E6-B by following these steps:
First, multiply 340 by 78 (disregard the minus sign) [Figure 3]:
• Step 1—place 10 on the inner scale (this is the index opposite 34 on the outer scale that represents 340).
• Step 2—opposite 78 on the inner scale, read 26.5 on the outer scale.
Determine the value of these digits by estimating: 300 × 80 = 24,000, so 340 × 78 = 26,500.
Then, divide 26,500 by 2,006 [Figure 4]:
• Step 3—on the inner scale, place 20, which represents 2,006 opposite 26.5 on the outer scale (26.5 represents 26,500).
• Step 4—opposite the index, 10, on the inner scale read 13.2 on the outer scale.
Determine the value of 13.2 by estimating: 20,000 ÷ 2000 = 10, so 26,500 ÷ 2,006 = 13.2.
The arm (–78) is negative, so the CG is also negative.
The CG is –13.2 inches or 13.2 inches ahead of the datum.
The problem just solved with an electronic calculator and an E6-B can also be solved with a dedicated flight computer using the information shown in Figure 2. Each fligh computer handles the problems in a slightly different way, but all are programmed with prompts that solicit the required data to be inputted so there is no need to memorize any formulas. Weight and arms are inputted as called for, and a running total of the weight, moment, and CG are displayed.
Use this formula:
1. Determine the CG in inches from the main wheel: (340)(×)(78)(÷)(2006)(=) 13.2
2. Determine the CG in inches form the datum: (128)(–)(13.2)(=) 114.8
The CG is 114.8 inches behind the datum.
Use this formula:
1. Determine the CG in inches from the main wheels: (340)(×)(78)(÷)(2006)(=) 13.2
2. Determine the CG in inches from the datum: (75)(+)(13.2)(=) 88.2
The minus sign before the parenthesis in the formula means the answer is negative. The CG is 88.2 inches ahead of the datum (–88.2).
Use this formula:
1. Determine the CG in inches from the main wheels: (67)(×)(222)(÷)(1218)(=) 12.2
2. Determine the CG in inches from the datum: (7.5)(+)(12.2)(=) 19.7
The CG is 19.7 inches behind the datum.
Use this formula:
1. Determine the CG in inches from the main wheels: (67)(×)(222)(÷)(1218)(=) 12.2
2. Determine the CG in inches from the datum: (80)(+/–)(+)(12.2)(=) –67.8
The CG is 67.8 inches ahead of the datum.
Determine the CG by using the data in Figure 6 and following these steps:
1. Determine the total weight and record this number: (830)(+)(836)(+)(340)(=) 2,006
2. Determine the moment of each weighing point and record them:
(830)(×)(128)(=) 106,240
(836)(×)(128)(=) 107,008
(340)(×)(50)(=) 17,000
3. Determine the total moment and divide this by the total weight: (106240)(+)(107008)(+)(17000)(=)(÷)(2006)(=) 114.8
This airplane weighs 2,006 pounds and its CG is 114.8 inches from the datum.
Determine the CG by using the data in Figure 7 and following these steps:
1. Determine the total weight and record this number: (830)(+)(836)(+)(340)(=) 2,006
2. Determine the total moment index, divide this by the total weight, and multiply it by the reduction factor of 100: (1062.4)(+)(1070.1)(+)(170)(=)(2302.5)(÷)(2006)(=)(1.148)(×)(100)(=) 114.8
This airplane weighs 2,006 pounds and its CG is 114.8 inches from the datum.
• MAC is 61.6 inches long.
• LEMAC is at station 20.1.
1. Determine the distance between the CG and LEMAC: (42.47)(–)(20.1)(=) 22.37
2. Then, use this formula: (22.37)(×)(100)(÷)(61.6)(=) 36.3
The CG of this airplane is located at 36.3 percent MAC.
Determine the lateral CG by using the data in Figure 8 and following these steps:
1. Add all of the weights: (1545)(+)(170)(+)(200)(+)(288)(=) 2,203
2. Multiply the lateral arm (the distance between butt line zero and the CG of each item) by its weight to get the lateral offset moment of each item. Moments to the right of BL 0 are positive and those to the left are negative.
(1,545)(×)(.2)(=) 309
(170)(×)(13.5)(+/–)(=) –2,295
(200)(×)(13.5)(=) 2,700
(288)(×)(8.4)(+/–)(=) –2,419
3. Determine the algebraic sum of the lateral offset moments.
(309)(+)(2295)(+/–)(+)(2700)(+)(2419)(+/–)(=) –1,705
4. Divide the sum of the moments by the total weight to determine the lateral CG.
(1705)(+/–)(÷)(2203)(=) –0.77
The lateral CG is 0.77 inch to the left of BL0.
1. Determine the number of inches the baggage is shifted: (246)(–)(118)(=) 128
2. Use this formula:
(50)(×)(128)(÷)(4709)(=) 1.36
The CG is shifted forward 1.36 inches.
1. Determine the number of inches the baggage is shifted: (246)(–)(118)(=) 128
2. Use this formula:
(2)(×)(4709)(÷)(128)(=) 73.6
Moving 73.6 pounds of baggage from the aft compartment to forward compartment shifts the CG forward 2 inches.
1. Use this formula:
(1.5)(×)(4026)(÷)(56)(=) 107.8
1. Moving the battery aft by 107.8 inches shifts the CG aft 1.5 inches.
1. Use this formula:
(500)(×)(96)(÷)(2)(=) 24,000
Moving 500 pounds of cargo 96 inches forward causes a 2.0-inch shift in CG of a 24,000-pound airplane.
1. Use this formula:
(1876)(×)(.8)(÷)(195)(=) 7.7
Attaching 7.7 pounds of ballast to the bulkhead at station 228 moves the CG to +33.0.
Electronic Calculator
Determining the CG of an airplane in inches for the main-wheel weighing points can be done with any simple electronic calculator that has addition (+), subtraction (–), multiplication (×), and division (÷) functions. [Figure 1] |
| Figure 1. A typical electronic calculator is useful for solving most types of weight and balance problems |
Scientific calculators with such additional functions as memory (M), parentheses (( )), plus or minus (+/–), exponential (yx), reciprocal (1/x), and percentage (%) functions allow more complex problems to be solved or simple problems to be solved using fewer steps.
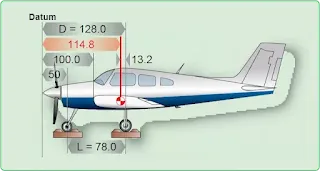
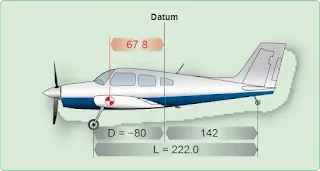
According to Figure 2, the weight of the nosewheel (F) is 340 pounds, the distance between main wheels and nosewheel (L) is –78 inches, and the total weight (W) of the airplane is 2,006 pounds. L is negative because the nosewheel is ahead of the main wheels.
According to Figure 2, the weight of the nosewheel (F) is 340 pounds, the distance between main wheels and nosewheel (L) is –78 inches, and the total weight (W) of the airplane is 2,006 pounds. L is negative because the nosewheel is ahead of the main wheels.
 |
| Figure 2. Weight and balance data of a typical nosewheel airplane |
To determine the CG, use this formula:
Key the data into the calculator and press the equal (=) key. The answer should read as follows: (340)(×)(78)(+/–)(÷)(2006)(=) –13.2
The arm of the nosewheel is negative, so the CG is –13.2 or 13.2 inches ahead of the main wheel weighing points.
E6-B Flight Computer
The E6-B uses a special kind of slide rule. Instead of its scales going from 1 to 10, as on a normal slide rule, both scales go from 10 to 100. The E6-B cannot be used for addition or subtraction, but it is useful for making calculations involving multiplication and division. Its accuracy is limited, but it is sufficiently accurate for most weight and balance problems.The same problem that was just solved with the electronic calculator can be solved on an E6-B by following these steps:
First, multiply 340 by 78 (disregard the minus sign) [Figure 3]:
 |
| Figure 3. E6-B computer set up to multiply 340 by 78 |
• Step 1—place 10 on the inner scale (this is the index opposite 34 on the outer scale that represents 340).
• Step 2—opposite 78 on the inner scale, read 26.5 on the outer scale.
Determine the value of these digits by estimating: 300 × 80 = 24,000, so 340 × 78 = 26,500.
Then, divide 26,500 by 2,006 [Figure 4]:
 |
| Figure 4. E6-B computer set up to divide 26,500 by 2,006 |
• Step 3—on the inner scale, place 20, which represents 2,006 opposite 26.5 on the outer scale (26.5 represents 26,500).
• Step 4—opposite the index, 10, on the inner scale read 13.2 on the outer scale.
Determine the value of 13.2 by estimating: 20,000 ÷ 2000 = 10, so 26,500 ÷ 2,006 = 13.2.
The arm (–78) is negative, so the CG is also negative.
The CG is –13.2 inches or 13.2 inches ahead of the datum.
Dedicated Electronic Flight Computer
Dedicated electronic flight computers, like the one in Figure 5, are programmed to solve many flight problems such as wind correction, heading and ground speed, endurance, and true airspeed (TAS), as well as weight and balance problems. |
| Figure 5. Dedicated electronic flight computers are programmed to solve weight and balance problems, as well as flight problems |
The problem just solved with an electronic calculator and an E6-B can also be solved with a dedicated flight computer using the information shown in Figure 2. Each fligh computer handles the problems in a slightly different way, but all are programmed with prompts that solicit the required data to be inputted so there is no need to memorize any formulas. Weight and arms are inputted as called for, and a running total of the weight, moment, and CG are displayed.
Typical Weight and Balance Problems
A hand-held electronic calculator like the one in Figure 5 is a valuable tool for solving weight and balance problems. It can be used for a variety of problems and has a high degree of accuracy. The examples given here are solved with a calculator using only the (×),(÷),(+),( – ), and (+/–) functions. If other functions are available on your calculator, some of the steps may be simplifiedDetermining CG in Inches From the Datum
This type of problem is solved by firs determining the location of the CG in inches from the main wheel weighing points, then measuring this location in inches from the datum. There are four types of problems involving the location of the CG relative to the datum.Nosewheel Airplane With Datum Ahead of the Main Wheels
The datum (D) is 128 inches ahead of the main wheel weighing points; the weight of the nosewheel (F) is 340 pounds, and the distance between main wheels and nosewheel (L) is 78 inches. The total weight (W) of the airplane is 2,006 pounds.
Use this formula:
1. Determine the CG in inches from the main wheel: (340)(×)(78)(÷)(2006)(=) 13.2
2. Determine the CG in inches form the datum: (128)(–)(13.2)(=) 114.8
The CG is 114.8 inches behind the datum.
Nosewheel Airplane With Datum Behind the Main Wheels
The datum (D) is 75 inches behind the main wheel weighing points, the weight of the nosewheel (F) is 340 pounds, and the distance between main wheels and nosewheel (L) is 78 inches. The total weight (W) of the airplane is 2,006 pounds.
Use this formula:
1. Determine the CG in inches from the main wheels: (340)(×)(78)(÷)(2006)(=) 13.2
2. Determine the CG in inches from the datum: (75)(+)(13.2)(=) 88.2
The minus sign before the parenthesis in the formula means the answer is negative. The CG is 88.2 inches ahead of the datum (–88.2).
Tailwheel Airplane With Datum Ahead of the Main Wheels
The datum (D) is 7.5 inches ahead of the main wheel weighing points, the weight of the tailwheel (R) is 67 pounds, and the distance between main wheels and tailwheel (L) is 222 inches. The total weight (W) of the airplane is 1,218 pounds.
Use this formula:
1. Determine the CG in inches from the main wheels: (67)(×)(222)(÷)(1218)(=) 12.2
2. Determine the CG in inches from the datum: (7.5)(+)(12.2)(=) 19.7
The CG is 19.7 inches behind the datum.
Tailwheel Airplane With Datum Behind the Main Wheels
The datum (D) is 80 inches behind the main wheel weighing points, the weight of the tailwheel (R) is 67 pounds, and the distance between main wheels and tailwheel (L) is 222 inches. The total weight (W) of the airplane is 1,218 pounds.
Use this formula:
1. Determine the CG in inches from the main wheels: (67)(×)(222)(÷)(1218)(=) 12.2
2. Determine the CG in inches from the datum: (80)(+/–)(+)(12.2)(=) –67.8
The CG is 67.8 inches ahead of the datum.
Determining CG, Given Weights, and Arms
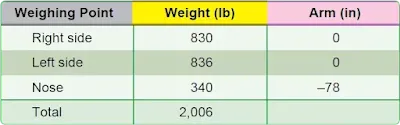
Some weight and balance problems involve weights and arms to determine the moments. Divide the total moment by the total weight to determine the CG. Figure 6 contains the specifications for determining the CG using weights and arms. |
| Figure 6. Specifications for determining the CG of an airplane using weight and arm |
Determine the CG by using the data in Figure 6 and following these steps:
1. Determine the total weight and record this number: (830)(+)(836)(+)(340)(=) 2,006
2. Determine the moment of each weighing point and record them:
(830)(×)(128)(=) 106,240
(836)(×)(128)(=) 107,008
(340)(×)(50)(=) 17,000
3. Determine the total moment and divide this by the total weight: (106240)(+)(107008)(+)(17000)(=)(÷)(2006)(=) 114.8
This airplane weighs 2,006 pounds and its CG is 114.8 inches from the datum.
Determining CG, Given Weights, and Moment Indexes
Other weight and balance problems involve weights and moment indexes, such as moment/100 or moment/1,000. To determine the CG, add all the weights and all the moment indexes. Then, divide the total moment index by the total weight and multiply the answer by the reduction factor. Figure 7 contains the specifications for determining the CG using weights and moments indexes. |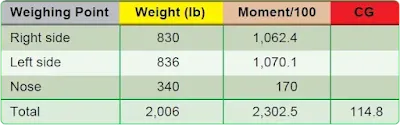
| Figure 7. Specifications for determining the CG of an airplane using weights and moment indexes |
Determine the CG by using the data in Figure 7 and following these steps:
1. Determine the total weight and record this number: (830)(+)(836)(+)(340)(=) 2,006
2. Determine the total moment index, divide this by the total weight, and multiply it by the reduction factor of 100: (1062.4)(+)(1070.1)(+)(170)(=)(2302.5)(÷)(2006)(=)(1.148)(×)(100)(=) 114.8
This airplane weighs 2,006 pounds and its CG is 114.8 inches from the datum.
Determining CG in Percent Mean Aerodynamic Chord (MAC)
• The loaded CG is 42.47 inches aft of the datum.• MAC is 61.6 inches long.
• LEMAC is at station 20.1.
1. Determine the distance between the CG and LEMAC: (42.47)(–)(20.1)(=) 22.37
2. Then, use this formula: (22.37)(×)(100)(÷)(61.6)(=) 36.3
The CG of this airplane is located at 36.3 percent MAC.
Determining Lateral CG of a Helicopter
For a helicopter, it is often necessary to determine not only the longitudinal CG, but the lateral CG as well. Lateral CG is measured from butt line zero (BL 0). All items and moments to the left of BL 0 are negative, and all those to the right of BL 0 are positive. Figure 8 contains the specifications for determining the lateral CG of a typical helicopter. |
| Figure 8. Specifications for determining the lateral CG of a helicopter |
Determine the lateral CG by using the data in Figure 8 and following these steps:
1. Add all of the weights: (1545)(+)(170)(+)(200)(+)(288)(=) 2,203
2. Multiply the lateral arm (the distance between butt line zero and the CG of each item) by its weight to get the lateral offset moment of each item. Moments to the right of BL 0 are positive and those to the left are negative.
(1,545)(×)(.2)(=) 309
(170)(×)(13.5)(+/–)(=) –2,295
(200)(×)(13.5)(=) 2,700
(288)(×)(8.4)(+/–)(=) –2,419
3. Determine the algebraic sum of the lateral offset moments.
(309)(+)(2295)(+/–)(+)(2700)(+)(2419)(+/–)(=) –1,705
4. Divide the sum of the moments by the total weight to determine the lateral CG.
(1705)(+/–)(÷)(2203)(=) –0.77
The lateral CG is 0.77 inch to the left of BL0.
Determining ΔCG Caused by Shifting Weights
Fifty pounds of baggage is shifted from the aft baggage compartment at station 246 to the forward compartment at station 118. The total airplane weight is 4,709 pounds. How much does the CG shift?1. Determine the number of inches the baggage is shifted: (246)(–)(118)(=) 128
2. Use this formula:
(50)(×)(128)(÷)(4709)(=) 1.36
The CG is shifted forward 1.36 inches.
Determining Weight Shifted to Cause Specified ΔCG
How much weight must be shifted from the aft baggage compartment at station 246 to the forward compartment at station 118 to move the CG forward 2 inches? The total weight of the airplane is 4,709 pounds.1. Determine the number of inches the baggage is shifted: (246)(–)(118)(=) 128
2. Use this formula:
(2)(×)(4709)(÷)(128)(=) 73.6
Moving 73.6 pounds of baggage from the aft compartment to forward compartment shifts the CG forward 2 inches.
Determining Distance Weight Is Shifted to Move CG a Specific Distance
How many inches aft does a 56 pound battery need to be moved to shift the CG aft by 1.5 inches? The total weight of the airplane is 4,026 pounds.1. Use this formula:
(1.5)(×)(4026)(÷)(56)(=) 107.8
1. Moving the battery aft by 107.8 inches shifts the CG aft 1.5 inches.
Determining Total Weight of an Aircraft With a Specified ΔCG When Cargo Is Move
What is the total weight of an airplane if moving 500 pounds of cargo 96 inches forward shifts the CG 2.0 inches?1. Use this formula:
(500)(×)(96)(÷)(2)(=) 24,000
Moving 500 pounds of cargo 96 inches forward causes a 2.0-inch shift in CG of a 24,000-pound airplane.
Determining Amount of Ballast Needed to Move CG to a Desired Location
How much ballast must be mounted at station 228 to move the CG to its forward limit of +33? The airplane weighs 1,876 pounds and the CG is at +32.2, a distance of 0.8 inch out of limit.1. Use this formula:
(1876)(×)(.8)(÷)(195)(=) 7.7
Attaching 7.7 pounds of ballast to the bulkhead at station 228 moves the CG to +33.0.
RELATED POSTS
- Light Sport Aircraft Weight and Balance Control
- Single Engine Aircraft Weight and Balance Computations
- Multiengine Aircraft Weight and Balance Computations
- Center of Gravity Change After a Repair or Alteration
- Weight and Balance Control - Helicopter
- Weight and Balance Control - Commuter Category and Large Aircraft
